Generalized Estimating Equation, GEE
前言
一般的線性迴歸模型在使用上有假設條件的限制,資料需符合常態、獨立和均質(變異數相同)的條件,當資料為重複測量資料又不符合常態分配時,
可以使用廣義估計方程式來推估迴歸系數和標準誤。以下會針對廣義估計方程式(Generalized estimating equation, GEE)進行基本介紹以及SPSS的範
例操作和說明。
廣義估計方程式(Generalized estimating equation, GEE)
一、是一種估計方法而非模型方法,且為半參數估計,沒有資料分佈的限制。
二、適用於長期追蹤資料、重複測量資料或集群資料。
三、反應變項(outcome)可為連續、類別、順序或計數類型。
四、容許遺失值存在,即使缺少多次測量中的某次資料,GEE仍會分析其他次的資料,不會整筆刪除
五、工作中相關性矩陣:設定多次測量資料之間的相關性。
1. 獨立(Independent):多次測量資料之間無相關性,同一人的重複測量資料之間通常具有相關性非獨立,因此獨立矩陣不適合用在重複測量
或長期追蹤的研究。
2. AR(1):一階自迴歸模型(First-order autoregressive),每一次測量資料都和前一次測量資料有關,間隔越多次,相關性越小。
3. 可交換(Exchangeable):多次測量資料之間有同質相關性。
4. M個相依:連續測量具有共用相關係數,由第三個測量分隔的測量配對具有共用相關係數,依此類推,直到由 m 1 其他測量分隔的測量配對。
例如,如果您每年為 3 年級到 7 年級的學生提供標準化測試。 此結構假設 3 年級與 4 年級、4 年級與 5 年級、5 年級與 6 年級和 6 年級與 7
年級評分將具有相同的相關性;3 年級與 6 年級和 4 年級與 7 年級將具有相同的相關性。 分隔大於 m 的測量假設為不相關。 選擇這個結構時,
請指定小於工作中相關性矩陣之順序的 m 值。(此部分參考IBM說明文件)
5. 非結構化(Unstructured):多次測量資料之間的相關性都不一樣
範例資料介紹
檔案來自Agresti(2002)的長期追蹤研究資料,對於兩種治療憂鬱症藥物的效果比較,共有340個病人,追蹤3次藥物治療紀錄,並記錄每次治療後的
憂鬱狀態,檔案可於此連結下載,變項說明如下:
- diagnose 憂鬱症嚴重程度診斷,mild(輕度)、severe(重度)兩種類別
- drug 治療藥物,standard(標準用藥)和new(新藥)兩種, 以標準用藥作為參考組(比較組)
- id 病人編號
- time 追蹤治療次數(測量次數)編號,0、1、2分別代表第幾次追蹤記錄
- depression 當下的憂鬱狀態,1為正常,0為異常
分析目的
比較兩種藥物對於憂鬱情況改善的療效,同時也將憂鬱症嚴重程度和治療次數放入模型中作為調整變項,控制其他變項對憂鬱狀態的影響。
操作與結果
一、執行步驟與分析的相關設定:(Figure1)
(A) 點選 分析→概化線性模式→概化估計方程式
(B) 重複 頁面設定
(C) 模式類型 頁面設定
(D) 回應 頁面設定
(E) 預測 頁面設定
(F) 模式 頁面設定
(G) 統計量 頁面設定
2. 輸出結果 分析結果判讀與說明1 (詳見Figure 2)
3. 輸出結果 分析結果判讀與說明2 (詳見Figure 3)
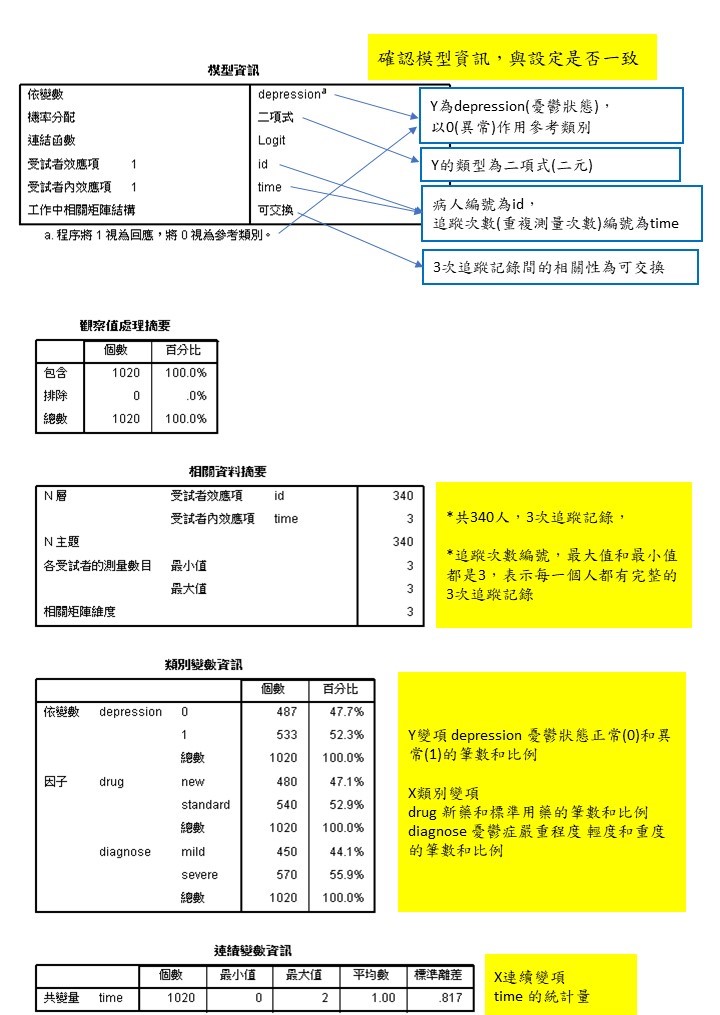
Figure 2 |
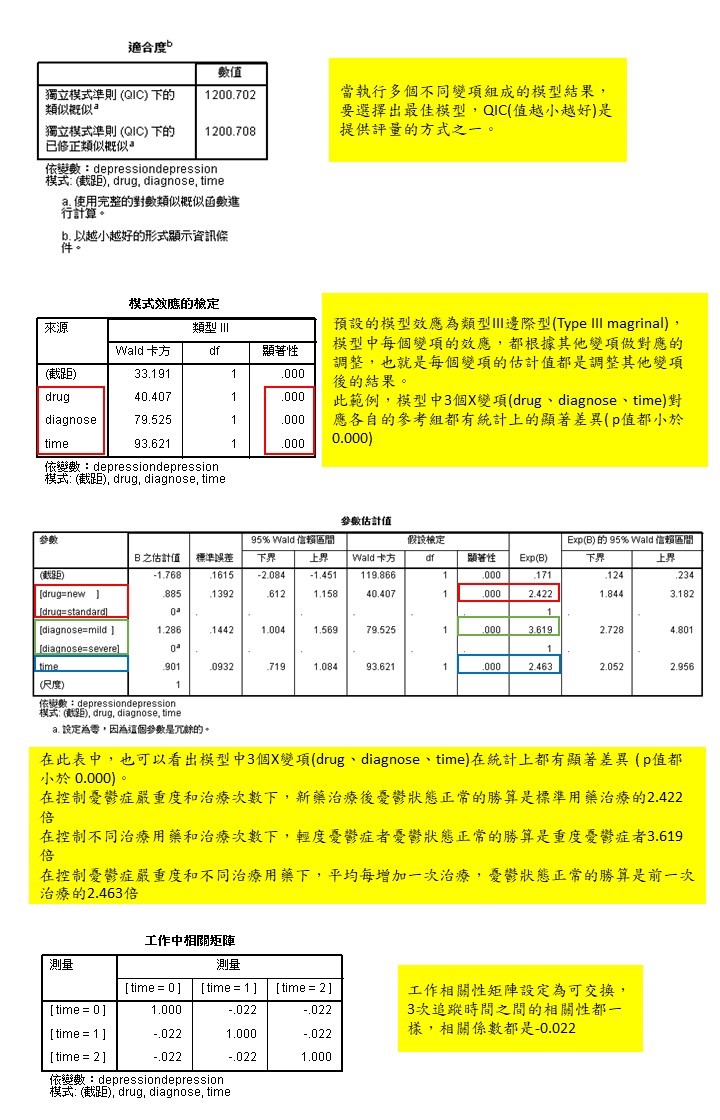
Figure 3 |


.JPG)
.JPG)
.JPG)

