Logistic Regression
前言
研究時,我們的依變項(Y)常分為有生病跟無生病兩類的類別變項,就不能使用簡單線性回歸來進行,這時我們要使用邏輯斯
迴歸分析(Logistic Regression Analysis)。
邏輯斯迴歸分析(Logistic Regression Analysis)
1. 此時依變數是一個二元(Binary)型態的類別資料,依變數其值僅為0或1。
2. 考量在不同的自變項(X)下,依變數為1比起依變數為0的勝算。
3. 經常借用換算後,以勝算比(odds ratio, OR)來呈現,OR會介於0~∞,1是標準值,小於1的會視為勝算(風險)低,大於1則
視為勝算(風險)高,請注意β係數≠勝算比(OR值)。
4. 基本公式為: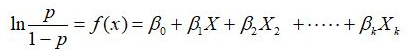
操作
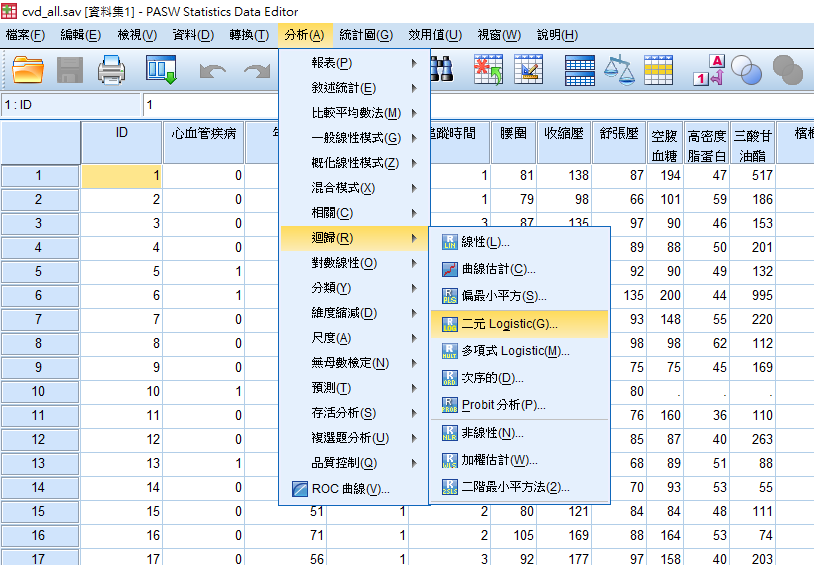
以下我們以收縮壓是否高於140 mm-Hg作為依變項(Y),是否喝酒作為自變項(X),並以年齡、性別、是否抽菸作為校正因子。
1. 請先確認依變數(Y)以定義為二元型態,通常0是無事件(如無生病)、1是有事件(如生病)。
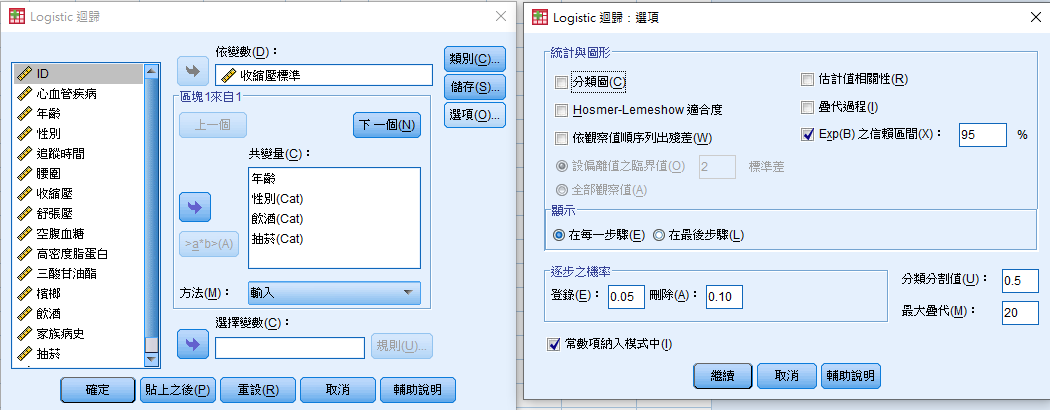
2. 操作如Figure 1(A),請注意選擇的是「二元Logistic」,下方的多項式Logistic指的是依變數不只二元,因此並非目前討論的方法。
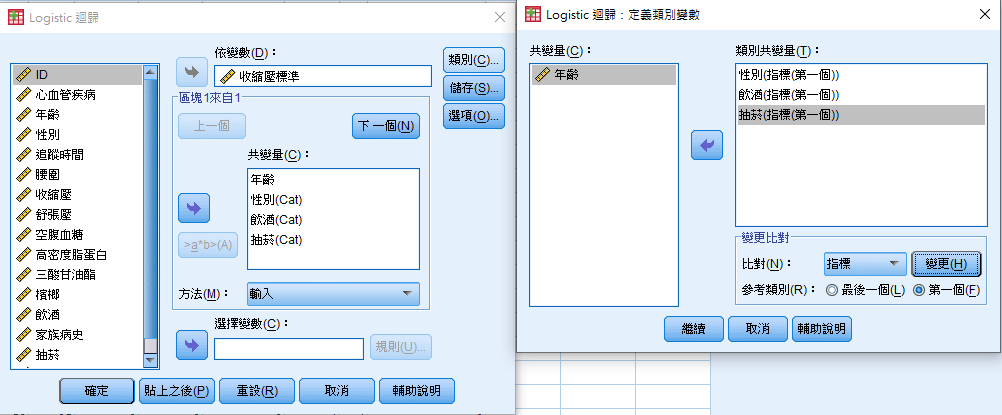
3. Figure 1(B)左邊是基本介面,在依變數放入依變數,下方的共變量則是自變數(X),可以只有1個,也可以多個,但請注意樣本數
是否足以分析這麼多變項。右邊的三個選項中,第一個類別點選後,需要將是類別變項放入右邊框框,接著下方的參考類別指的是
reference group,在此範例中,皆是將沒有該事件的人設定為0(如沒有抽菸),因此設定為「第一個」,記得按下「變更」,上方的
變項就會變成圖如所示後面多了(指標(第一個))。
4. 在「選項」中,可以點選Exp(B)之信賴區間估計,就可以請SPSS一同計算出勝算比(OR值)的95%CI。
結果
因為輸出的表格很多,以下會擷取重點結論的部分來進行簡單的說明:
1. 首先,觀察值處理摘要(Figure 2(A)),可以先確認一下到底有多少樣本納入計算,避免掉很多樣本因為資料缺失被刪除,可能會影
響到回歸方程式的估計。
2. 其次,在類別變數編碼的表格(Figure 2(B))會呈現類別變項中每組別有多少個案,以及在回歸中的參考編碼,如0則是參考組。另外
若是類別變項不是以數字編碼,像是女性為F、男性為M的話,也可以從此表格中確認參考組的設定狀況。
3. Figure 2(C)呈現若是以此模型來預測有沒有生病的結果,以此範本為例,有81%的狀況是被預測正確的。
4. 最後,在「變數在方程式中」這個表格(Figure 2(D))可看到方程式結果,Exp(B)是已經經由計算後得到的勝算比(OR值),若是先前在
「選項」中已勾選計算信賴區間的話,就會在最後面呈現。
5. 以喝酒這個變項為例,解釋如下:在控制了其他條件(年齡、性別、抽菸)下,有喝酒的人比起沒有喝酒的人發生收縮壓>140 mm-Hg
風險是1.407倍,並且達統計上顯著差異(P-value<0.001)。


.JPG)