首頁 二級單位 健康資料加值暨統計中心 統計軟體操作 回歸 Linear regression
  • 尋找：

健康資料加值暨統計中心

Linear Regression
 
前言

       一個變數對於另外一個變數的影響，或者多個變數對一個變數的影響，經常利用線性回歸來表示其影響力，或作為數值的預測。以下會

針對簡單線性回歸(Simple linear regression)以及多變項線性回歸(Multiple linear regression)來進行SPSS的操作。

線性回歸(Simple linear regression)

       一、可以用來估計(estimation)或是預測(prediction)，當X(自變項)增加一單位則Y(依變項)增加多少單位。
       
       二、是利用數筆觀察值去找到一個回歸方程式，且能離各觀察點最近的(最小平方法, least-squares method)

       三、方程式為：ŷ=ß0+ß1+ε ， 是Ｙ軸截距(y-axis intercept)， ε為殘差或者稱y的誤差(error)

       四、本假設及檢定方式：

           1. 資料為線性相關：X與Y呈現直線關係，所以若Y為二分(如有無生病)則不適用。
               →利用殘差圖判斷

           2. 獨立性：每一筆資料是獨立的，因此不適用於重複測量
               →利用殘差圖判斷

           3.常態性：資料須成常態，X不管是任何數值的情況下，Y都必須符合常態分佈
               →利用P-P圖判斷

           4.變異數相同：: 變異數若不相等會導致自變數無法有效估計依變數
              →利用殘差圖判斷

       五、判定係數(R2)
           
           1.或者稱決定係數(Coefficient of Determination)，Y可以被X解釋的百分比，百分比越高表示X對於Y的影響力越大。

           2. R2=可由獨立變數解釋之變異/總變異 ，0≦ R2 ≦1，在Figure 1中可以看到左邊的圖R2是81%，比右圖的R2大，具有比較好的解釋

           力，觀察值也都比較靠近方程式。

           3.不具外推性、也不具因果性：如果原本資料中舒張壓的範圍是40～140，那如果要推估舒張壓是150時，結果可能不準確，另外沒有

           考量到時間問題，因此不具因果性。

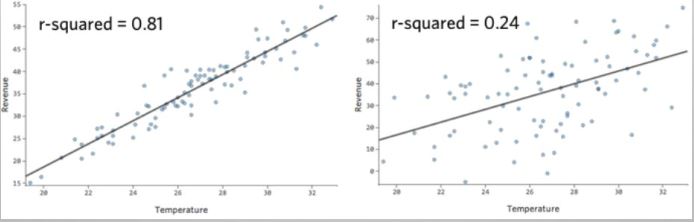Figure 1
 
簡單線性回歸(Simple linear regression)

       一、只觀察兩個變項之間的關係，例如：年齡與高血壓、血糖與膽固醇

       二、R2=(簡單相關係數)2=r2

       三、數值解釋與皮爾森相關係數相同

多變項(複)線性回歸(Multiple linear regression)

       觀察多個變項數值對於依變項的影響，例如同時考慮年齡、性別、舒張壓去預測收縮壓

X是類別變項該怎麼辦
       
       如果類別變項超過2個類別時，須將變項拆開，例如地區分成北、中、南、東，這時就需要設置dummy variable，可以利用分組的方式來

進行，若是本版為22版以上，可以使用轉換中的建立虛擬變數，例如：抽菸量中，包含了0(不抽)、1(一天一包)、2(一天一包以上)

，因此我們需要新成兩個變項，將他拆解為以下：
 
0→ X1:0   X2:0
1→ X1:1   X2:0
2→ X1:0   X2:1

在分析時再一起放入分析中。

操作與結果
       
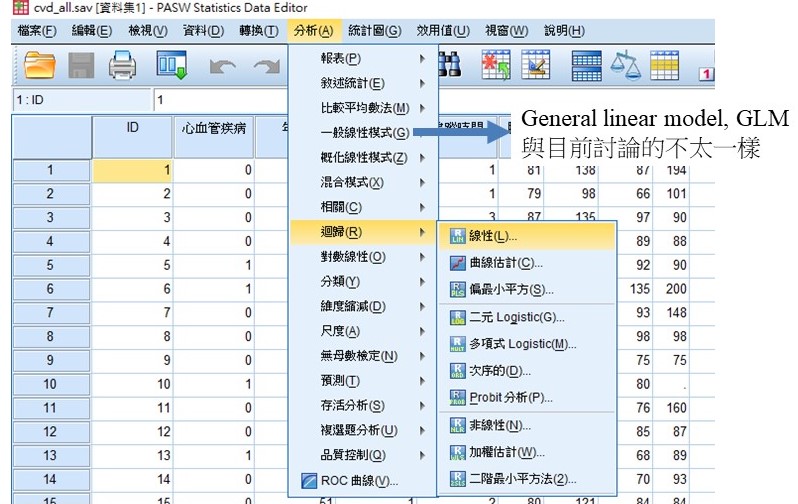
       基本操作如Figure 2，請記得若是類別變項，要將該變項所有的dummy variable都放入，細部的調整如Figure 3。
       
       Figure 4 中呈現的是簡單線性回歸的結果，是以舒張壓來預測(估計)收縮壓，第一個表格會附上變項之間的相關性，接著可以跳到第三個

表格的模型摘要，這裡的R2為0.552，表示舒張壓可以估計55.2%的收縮壓變異。ANOVA顯著性結果為0.000，表示自變項對於依變項有顯著的

解釋性，最後一個係數的表格，呈現的是整個模型(方程式)的相關係數，一般而言顯著性小於0.05會視為該係數有統計意義，以此結果而言，若

要預測收縮壓，方程式為22.582+1.289*舒張壓=收縮壓，若要有一個案的舒張壓為80，22.582+1.289*80=125.702，表示以此模型估計此個案

的收縮壓會是125.702。

       Figure 5中以更多變項來預測收縮壓，包含了舒張壓、年齡、性別，這裡的性別只有兩個選項，且已經以0、1來編碼，因此不需要另外設dummy。

與Figure 4的單一變項估計比較，這裡可以發現解釋力(R2)變高了，係數解釋則是與Figure 4相同。
 
(A)

(B)
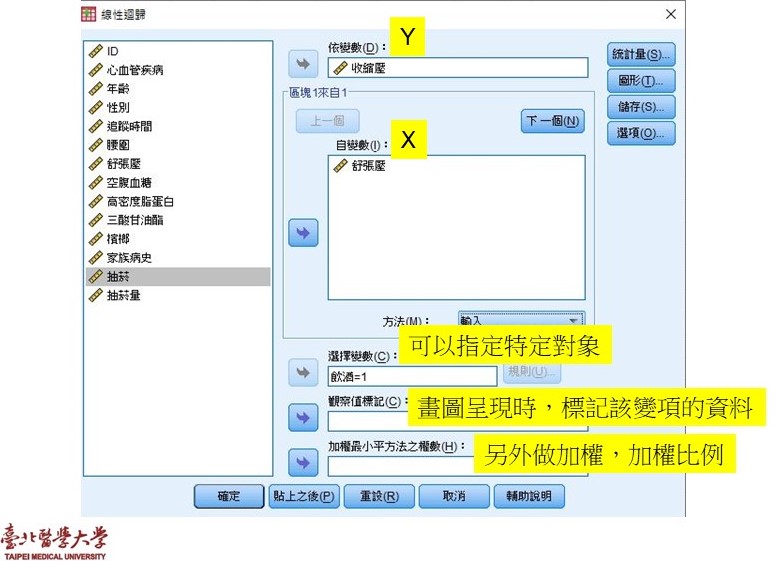
Figure 2
 
 (A)

(B)

(C)
 Figure 3
 
 
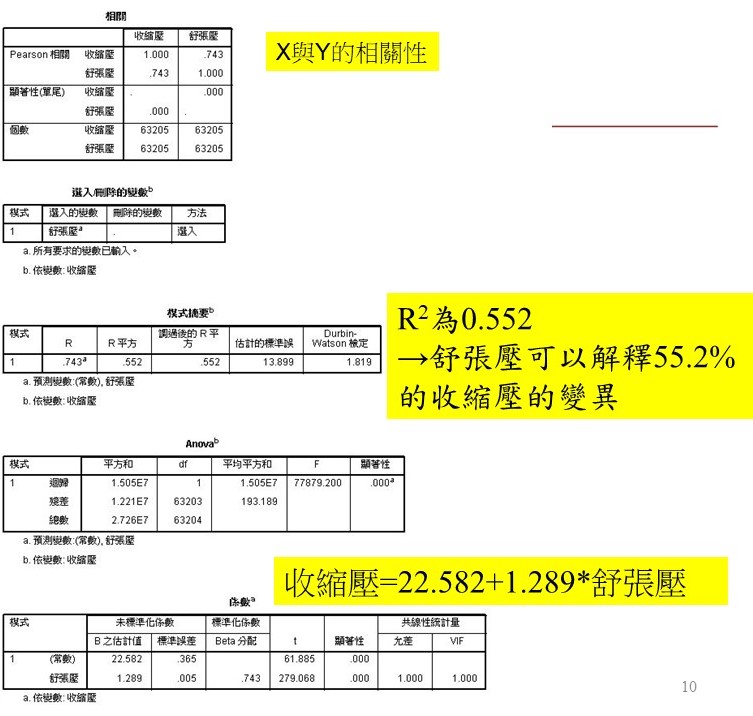
 Figure 4
 
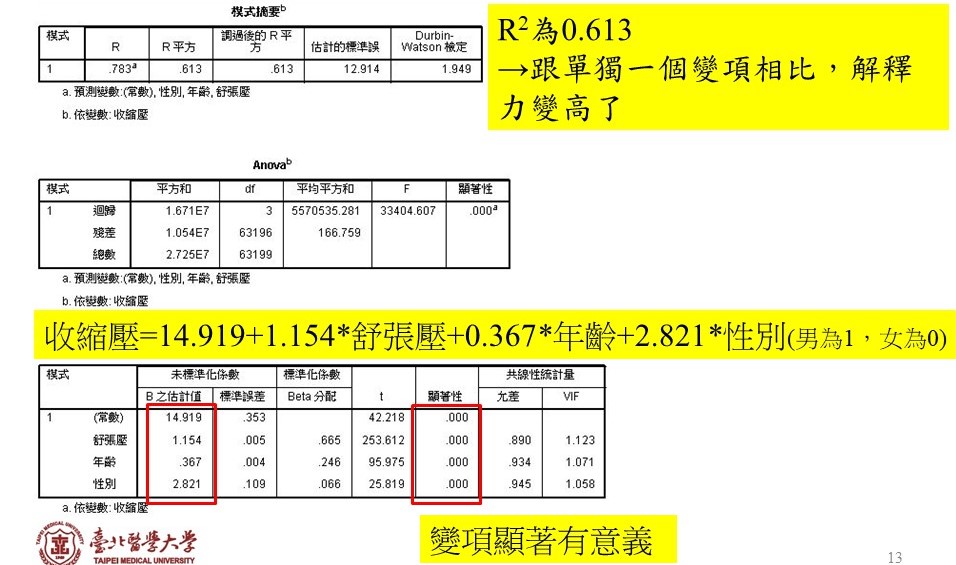
Figure 5
 

使用規則

  1. 本網站所刊載資料之著作權，除另有規定外，屬於 臺北醫學大學 數據處（下稱「本單位」）。任何人得為非營利目的自由使用。但使用時，不得變更其內容、詆毀或減損本單位名譽，且必須註明來源為「臺北醫學大學 數據處」。
  2. 具有上傳資料權限之使用者，得自行決定其資料之著作權歸屬與授權規則。本網站之使用者，應遵守之，並了解本單位對此資料不負任何法律責任。
  3. 本單位盡力維護本網站資料之即時性與正確性，但對此不負任何責任。本單位有權不經事先公告，變更網站內容。因此，凡使用者認為涉及其利益之事項，例如使用資格或日期等，請逕與本單位相關業務人員確認。
  4. 本單位盡力維護本網站資料不含任何電腦病毒。但對於任何因下載本網站資料所致電子資訊系統或其他之損害，本單位不負任何責任。
  5. 本網站所提供對其他網站之超連結，僅為使用者之便利。該被連結之他網站，並非本網站之一部分。本單位不保證所連結之他網站存在，亦不對該網站之任何內容、超連結等負責。
  6. 本網站除為提供個人服務之必要外，不使用 cookies ，也不追蹤使用者之網路使用。使用者主動提供之個人資料，除指定目的與分析本網站使用習慣外，不作其他用途。
  7. 本使用規則之修改變更，不預先公告。若使用者對於本規則或本網站有任何意見或建議，請聯繫我們。