相關性
前言
在兩個連續變數中,常需要驗證兩者之間的關係,一般而言指的是線性相關,有時當一個變數變大,另一個也隨之增大,又或一個變大,另外一個
隨之減小,這樣的線性關係我們可以藉由皮爾森相關係數Pearson’s Correlation Coefficient或是斯皮爾曼等級相關係數Spearman’s rank correlation
coefficient來進行檢定。
皮爾森相關係數Pearson’s Correlation Coefficient
一、母群相關係數代號ρ,樣本相關係數代號r,是用來討論兩個連續變數的相關性,沒有單位,數值會介於1~-1之間,係數不能夠做因果的推論,
使用時須要滿足以下條件:
1. 每對資料均為獨立
2. 資料呈常態分布
3. 相同變異數
4.X與Y的關係為直線
二、當1≧r> 0 為正相關,-1≦r<0 負相關,依照領域的不同,對於相關係數的強弱判定不一,以下判定僅供參考
1. r值於0~0.25或0~ -0.25 → 兩者缺乏相關
2. r值於0.25~0.50或-0.25~ -0.5 → 兩者相關不強
3. r值於0.5~0.75或-0.5~ -0.75 → 兩者適度或良好相關
4. r值於0.75~1.0或-0.75~ 1.0 → 兩者相關係非常好
斯皮爾曼等級相關係數Spearman’s rank correlation coefficient
是一種無母數分析法,將X及Y資料取序位(rank)後,再去計算彼此間的相關係數,適用於沒有常態分佈的數值,或是次序變項,優點是不受極端
值影響,數值解釋與皮爾森相關係數相同
操作與結果
在進行相關係數檢定前,請先檢定資料是否呈常態分佈,以選擇適合的相關係數,請點選分析→相關→雙變數(Figure 1),進到雙變數相關分析畫
面後,便可將要進行相關性分析的變項一起放入變數中,接著就可以在相關係數中勾選要的方式,這裡的相關係數指的是皮爾森相關係數。
Figure 2的(A)是Pearson相關係數結果、(B)是Spearman’s 相關係數,兩個表格會長的一樣,解讀方式也相同。從左上到右下格子相關性皆是1,
兩邊的結果會是對稱的,以(A)中的空腹血糖和腰圍為例,相關性為0.2,顯著性是小於0.000,表示兩個呈顯著相關,但相關性只有0.2,在這兩種相關
性檢定,當人數很多時,都很容易達顯著,因此可以藉由相關係數再來下結論。(B)圖中收縮壓與舒張壓的相關係數是0.742,顯著性是小於0.000,表示
兩者呈現顯著相關,且兩者間有不錯的正相關性。
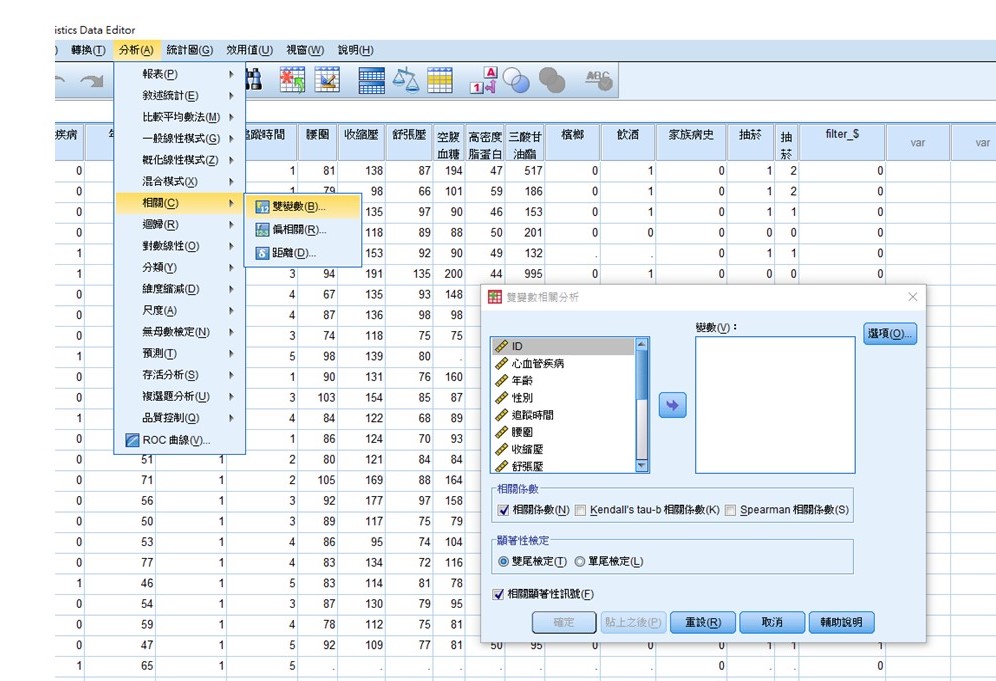
Figure 1 |
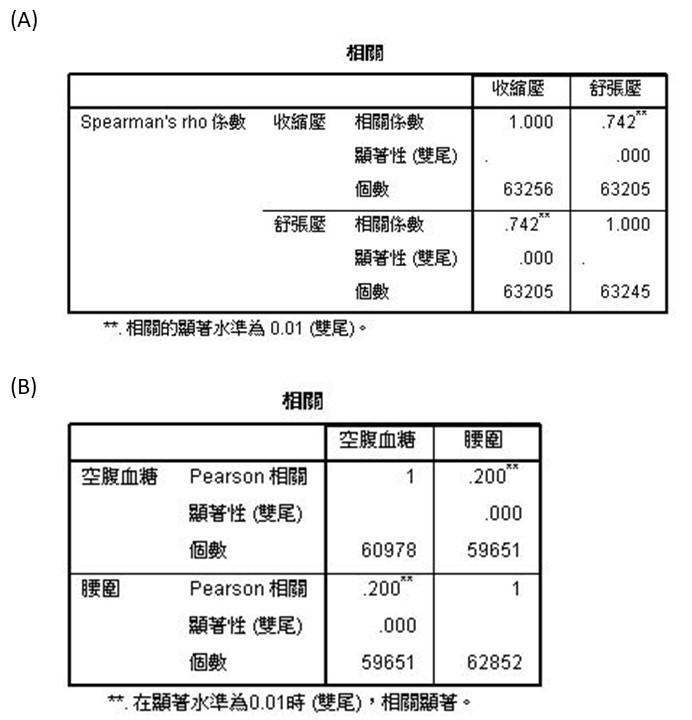
Figure 2 |



